One of the wonderful(?) things about Objective-C is that it’s based on C. Part of the power of C is bit-bashing, where you can manipulate individual bits inside of a piece of memory. Have a bunch of boolean values but don’t feel like wasting a byte or two for each one? Represent them as individual bits! Luckily we tend not have to do this a lot of these days given the massive amounts of memory that we have to play with, even on iOS devices. That being said, there are times where bitwise operations appear in the Cocoa APIs, so it’s good to be comfortable with a couple of basic operations.

TL;DR:

• Combine bit flags with bitwise-OR, with a single pipe:

NSRegularExpressionCaseInsensitive | NSRegularExpressionUseUnixLineSeparators

• Test bit flags with bitwise-AND, with a single ampersand:

if (regexflags & NSRegularExpressionCaseInsensitive) { ...

• Clear flags with bitwise-ANDing the complement, using the twiddle ~:

regexflags = regexflags & ~NSRegularExpressionUseUnixLineSeparators

The tools

There are four basic tools in our bit twiddling arsenal

• shifting

• ORing

• ANDing

• NOTing

Shifting lets you slide bits to the left and to the right. This lets you position bits exactly where you want. The << and >> operators are used to shift bits. We’ll only be looking at <<, the left-shift operator because it’s useful for indicating which particular bit is interesting.

Say you had a bit pattern like this:

00101010. This is hex 0x2A, or decimal 42.

An expression like

0x2A << 2

Means to take the bits of 0x2A and scoot them to the left by two spots, fill in the bottom parts with zeros, and drop the top bits on the floor. The resulting pattern will be:

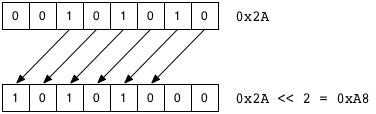
10101000, which is hex 0xA8, or decimal 168

ORing lets you combine two bit patterns together to form a third pattern.

In a bit pattern, a bit is said to be “set” if it has a value of 1, and “clear if it has a value of zero. With a bitwise OR, resulting pattern has bets set to 1 if either of the original patterns have a 1 bit, otherwise the bit is zero if both of the original patterns have a zero bit.

Hex 0x2A’s pattern is: 00101010, and the pattern 11010010 is hex 0xD2, the resulting bit pattern if they’re OR-d together will be 11111010, which is hex 0xFA, or decimal 250.

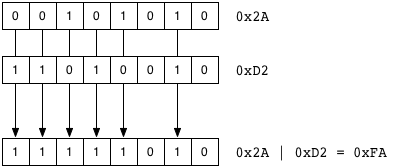
The syntax is the single pipe between integers: So, 0x2A | 0xD2 == 0xFA

OR is a very encompassing, friendly, gregarious operator. It’ll accept one-bits from anywhere. Got two bits set in the same position? No problem, it’s still set in the result.

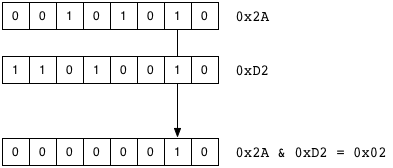
AND is like OR’s grumpy brother. AND is very discriminating about what bits it lets through. Given two bit patterns, a bit is set in the resulting pattern only_if the bit exists in both of the original two patterns.

The syntax is a single ampersand between two integers. Recall 0x2A is 00101010 and 0xD2 is 11010010, the result of 0x2A & 0xD2 will be 00000010, which is hex 0x02, or decimal 2. Notice that only one bit survived the journey:

NOT is the contrarian. Give NOT a single bit pattern, and you’ll get back its inverse. What was set is now clear, and what was clear is now set. (A bitwise koan?)

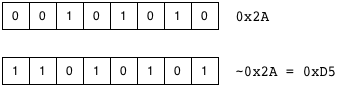
The bitwise-NOT syntax is a tilde/twiddle before a value: ~0x2A says to flip the bits of 0x2A (00101010) with a resulting value of 11010101, which is hex 0xD5:

With these four tools, you can address any particular bit in a chunk of memory, test its value (is it set or not?) and change its value (clear this here bit, or set that there other bit).

Optional Equipment

Option flags is the main place you’ll see exposed bits in Cocoa. These flags let you pack a lot of parameters into a small piece of memory, without needing to create method calls that take a lot of parameters, or supply a supplemental data structure such as a dictionary.

Consider this declaration from NSRegularExpression:

typedef NS_OPTIONS(NSUInteger, NSRegularExpressionOptions) {
   NSRegularExpressionCaseInsensitive             = 1 << 0,
   NSRegularExpressionAllowCommentsAndWhitespace  = 1 << 1,
   NSRegularExpressionIgnoreMetacharacters        = 1 << 2,
   NSRegularExpressionDotMatchesLineSeparators    = 1 << 3,
   NSRegularExpressionAnchorsMatchLines           = 1 << 4,
   NSRegularExpressionUseUnixLineSeparators       = 1 << 5,
   NSRegularExpressionUseUnicodeWordBoundaries    = 1 << 6
};

(OBTW, what is that NS_OPTIONS in the declaration? It just expands into an enum at compile time. Xcode, though, can look at NS_OPTIONS declarations and know that bit flags are involved, and kick in some extra type checking. Check out NSHipster for more details.)

This enum is composed of a bunch of bit flags. Recall the << operator, “left shift” takes a starting value and then moves all the bits to the left, filling in the bottom bits with zeros. With an expression like

1 << 0

The value of “1” (which is a single bit set):

00000001

Gets moved over zero positions, leaving the value unchanged:

00000001

1 << 1 says to take the single-bit number one:

00000001

and then move it over by one position, filling in zeros in the bottom position:

00000010

So, 1 << 1 is another way to say “2”. Or hexadecimal 0x02

Now 1 << 5. This means, take the number one:

00000001

and move it left five positions:

00100000

This value is 32 (decimal),or 0x20 (hex)

Here is that table of flags, along with their binary and hex representation:

typedef NS_OPTIONS(NSUInteger, NSRegularExpressionOptions) {
   NSRegularExpressionCaseInsensitive             = 1 << 0,   00000001   0x01
   NSRegularExpressionAllowCommentsAndWhitespace  = 1 << 1,   00000010   0x02
   NSRegularExpressionIgnoreMetacharacters        = 1 << 2,   00000100   0x04
   NSRegularExpressionDotMatchesLineSeparators    = 1 << 3,   00001000   0x08
   NSRegularExpressionAnchorsMatchLines           = 1 << 4,   00010000   0x10
   NSRegularExpressionUseUnixLineSeparators       = 1 << 5,   00100000   0x20
   NSRegularExpressionUseUnicodeWordBoundaries    = 1 << 6    01000000   0x40
};

You can see there is an individual bit position for each of these different possible behaviors. By constructing a pattern of bits you can exert a lot of control over your regular expression. Do this stuff long enough, and you can recognize bit patterns just from the hexadecimal values.

These constants are known as “bit masks”. They’re values that have bits set in particularly interesting positions. We can take an individual bit mask, like NSRegularExpressionCaseInsensitive and use it to twiddle that individual bit in some piece of memory, such as a method parameter.

Using the Options

Great. We have a pile of constants now describe bit positions. What next? You use these bit masks when you create a new regular expression object with +regularExpressionWithPattern:

+ (NSRegularExpression *) regularExpressionWithPattern: (NSString *) pattern
    options: (NSRegularExpressionOptions) options
    error:(NSError **)error;

You supply the regex pattern string in the first argument, then pick the options that govern the regular expression’s behavior and combine them together. Say you wanted to match things without caring about case. You’d use NSRegularExpressionCaseInsensitive. Pretend that you’re also dealing with a specially formatted text file such that n characters count as line breaks but not r. You might have r characters embedded in strings in a CSV and you’d want to ignore those if you’re processing the file on a line-by-line basis. The flag of interest is NSRegularExpressionUseUnixLineSeparators.

How do you use them? You combine the bit masks together. Bitwise-OR is the tool for combining – remember that OR is friendly and all-encompassing. We’ll get a bit mask with those two bits set by providing these two masks (CaseInsensitive and UnixLineSeparators) in an OR expression:

NSRegularExpression *regex =
    [NSRegularExpression regularExpressionWithPattern: ...
    options: NSRegularExpressionCaseInsensitive | NSRegularExpressionUseUnixLineSeparators
    error:...];

Here’s that expression again:

NSRegularExpressionCaseInsensitive | NSRegularExpressionUseUnixLineSeparators

The preprocessor replaces the human-readable names with their values:

1 << 0 | 1 << 5

And then the compiler precalculates the values, because they’re constants:

00000001 | 00100000

Thanks to C’s operator precedence rules, you don’t need any parentheses in that expression.

Here is the final binary bit mask:

00100001

Which is hex 0x21

+regularExpressionWithPattern can now look at 0x21’s bit pattern and figure out how you want it to behave.

A common error is to add these flags together rather than bitwise-ORing them. You’ll get the correct value in many cases. NSRegularExpressionCaseInsensitive + NSRegularExpressionUseUnixLineSeparators will also give you the value 0x21, but that’s a bad habit to get into because it can lead to subtle bugs. Consider this sequence of operations using NSRegularExpressionCaseInsensitive, which has the value of “1”

NSUInteger bitmask = 0x00;
bitmask = bitmask | NSRegularExpressionCaseInsensitive;
bitmask = bitmask | NSRegularExpressionCaseInsensitive;

The resulting value is going to be 0x01, with a single set bit on the bottom. Setting a bit that’s already set is a no-op.

But, if you use addition:

NSUInteger bit mask = 0x00;
bitmask = bitmask + NSRegularExpressionCaseInsensitive;
bitmask = bitmask + NSRegularExpressionCaseInsensitive;

The value of bitmask is now 0x02, which is NSRegularExpressionAllowCommentsAndWhitespace, and probably not what you want.

This isn’t a big deal when you’re just hard-coding a set of flags in a method call. But it can really bite you if you end up passing a bit mask around and are wanting to set your own bits in it.

Testing, Testing, 1-2-3

Setting flags is pretty easy. And for the most part, that’s all you have to deal with as Cocoa programmers – assemble the flags for the options you want and pass it into some method. But what if you want to write your own method that can interpret one of these packed-flags values? Similarly, what if you need to dissect a value returned from Cocoa that’s actually a bit pattern such as the current state of a UIDocument?

You test individual flags by using the bitwise-AND operator, which is a single ampersand: &

So say you’re handed a bit mask:

NSUInteger bit mask = 0x55;

And you want to see if the NSRegularExpressionCaseInsensitive is set. You would do something like:

if (bitmask & NSRegularExpressionCaseInsensitive) {
    // ignore case
}

Recall that bitwise AND looks at two bit patterns (0x55, which is 01010101, and NSRegularExpressionCaseInsensitive, which is 0x01, bit pattern 00000001) and makes a new, third bit pattern. Bits are set in the new pattern only if the corresponding bits are set in the two bit patterns. Have a diagram:

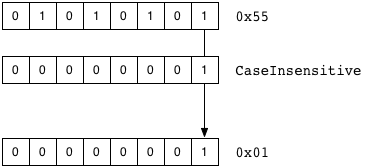
The resulting value is non-zero, so it’ll evaluate to true in the if statement above.
What about the other case, where that flag isn’t set? Say you started out with another bit mask, 0xFE, with a bit pattern of 11111110. All the bits are set except for NSRegularExpressionCaseInsensitive. The result of the AND expression is zero, which will interpreted as false:

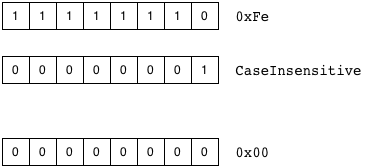
There is not a single bit that exists in both parts of the expression, so the result is zero.

Clearing Flags

Clearing flags is the last part of this bit flag extravaganza. Say you’re manipulating the accessibility traits on an object in your iOS app. You have a view that can be “adjustable” at times (its value can be manipulated), and static at other times. You’ll want to change your accessibilityTraits (which is a bit pattern) and turn the UIAccessibilityTraitAdjustable flag on and off. Turning it on is easy:

self.accessibilityTraits |= UIAccessibilityTraitAdjustable;

You can combine the bitwise operators with the assignment operator, letting you use something like |= exactly like you’d use +=.

Clearing a bit, though, is more work. It’s actually a two step process. Consider the tools at our disposal. Can bitwise-OR be used to test the flags? Not really. OR combines two bit patterns and forms their union. It’s hard to single someone out when the crowd just keeps getting bigger.

That leaves bitwise-AND. AND works like intersection. Maybe we could intersect the original value with a mask that would let every bit through except for the bit we want to clear. How to construct that mask?

Bitwise-NOT to the rescue! Hopping back to regular expressions for a second, NOT-ing a mask like NSRegularExpressionCaseInsensitive gives you a mask that has all bits set, except for the magic bit for the CaseInsensitive value:

What happens if you AND this value with another bit mask, like 0x55 (01010101)

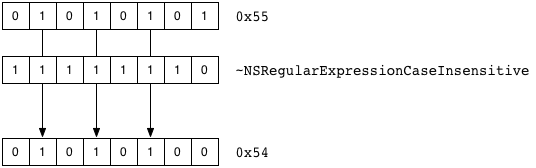
All the set-bits survive, except for CaseInsenstive. You’ve now cleared out the bit specified by the CaseInsensitive mask!

Applying this back to accessibility, you would clear the adjustable bit by doing:

self.accessibilityTraits &= ~UIAccessibilityTraitAdjustable;

If you think that looks weird, you’re right. But after you’ve done this stuff for awhile, you’ll be able to walk up to code like this and immediately grok its semantics: clear that particular bit.

Playing with this live

One of the best ways to learn this stuff is to play around with it. You can write little one-off programs and print out values. An interesting exercise is printing out the bit pattern for an integer. You can also purchase “computer-science calculators”, such as my beloved HP-16C and their apps that do the same thing.

But don’t forget that you have an interactive bit masher already installed on your machine: lldb and/or gdb. You can run the debugger from the command line and use it like a shell to explore the bitwise operations. The print command is the key. It will evaluate expressions, and will also let you decorate the command with a type specifier: /x for hex, /d for decimal, and /t for binary. Want to see the result of a shift?

$ lldb
(lldb) <strong>print/t 1<<5</strong>
(int) $1 = 0b00000000000000000000000000100000

That’s an annoying number of zeros. If you want to see just one byte’s worth, cast it to a char:

(lldb) <strong>print/t (char)(1<<5)</strong>
(char) $3 = 0b00100000

Play with bitwise-OR:

(lldb) <strong>print 0x2A | 0xD2</strong>
(int) $4 = 250
(lldb) <strong>print/t 0xFA</strong>
(char) $5 = 0b11111010
(lldb) <strong>print/x $5</strong>
(int) $5 = 0x000000fa

What’s that $3, $4 business? Every time you calculate or print a value, it gets assigned to a new variable that you can reference in later expressions.

That’s all folks

I hope you’ve enjoyed this brief romp through basic bitwise operators. Like them or not, they’re used in Cocoa, so it’s good to be familiar with them. To know why adding bit flags is generally a bad idea, and to know what you need to do (or at least know where to look up) to set and clear bits in a chunk of memory.